I. Wprowadzenie
Woda może zapalić świece. Czy to prawda? To prawda!
Czy to prawda, że węże boją się realgaru? To nieprawda!
Dzisiaj omówimy następujące kwestie:
Czy to prawda, że zakłócenia mogą zwiększyć dokładność pomiarów?
W normalnych warunkach interferencja jest naturalnym wrogiem pomiaru. Interferencja obniża dokładność pomiaru. W skrajnych przypadkach pomiar nie zostanie przeprowadzony prawidłowo. Z tej perspektywy interferencja może poprawić dokładność pomiaru, co jest nieprawdą!
Czy jednak zawsze tak jest? Czy zdarzają się sytuacje, w których zakłócenia nie obniżają dokładności pomiaru, a wręcz ją poprawiają?
Odpowiedź brzmi: tak!
2. Umowa o ingerencji
W związku z zaistniałą sytuacją, zawieramy następujące porozumienie w sprawie ingerencji:
- Zakłócenia nie zawierają składowych stałych. W rzeczywistych pomiarach zakłócenia są głównie zakłóceniami przemiennymi, co jest uzasadnione.
- W porównaniu ze zmierzonym napięciem stałym amplituda zakłóceń jest stosunkowo niewielka. Jest to zgodne z rzeczywistą sytuacją.
- Zakłócenie to sygnał okresowy lub średnia wartość równa się zero w ustalonym okresie czasu. Ten punkt niekoniecznie jest prawdziwy w rzeczywistych pomiarach. Ponieważ jednak zakłócenie jest zazwyczaj sygnałem prądu przemiennego o wyższej częstotliwości, w przypadku większości zakłóceń konwencja zerowej średniej jest uzasadniona przez dłuższy okres czasu.
3. Dokładność pomiaru w warunkach zakłóceń
Większość elektrycznych przyrządów pomiarowych i mierników wykorzystuje obecnie przetworniki AD, a ich dokładność pomiaru jest ściśle związana z rozdzielczością przetwornika AD. Ogólnie rzecz biorąc, przetworniki AD o wyższej rozdzielczości charakteryzują się wyższą dokładnością pomiaru.
Jednakże rozdzielczość AD jest zawsze ograniczona. Zakładając, że rozdzielczość AD wynosi 3 bity, a najwyższe napięcie pomiarowe wynosi 8 V, przetwornik AD jest równoważny skali podzielonej na 8 działek, z których każda wynosi 1 V. Wynik pomiaru tego AD jest zawsze liczbą całkowitą, a część dziesiętna jest zawsze przenoszona lub odrzucana, co jest przyjęte w niniejszym artykule. Przenoszenie lub odrzucanie spowoduje błędy pomiaru. Na przykład, 6,3 V jest większe niż 6 V i mniejsze niż 7 V. Wynik pomiaru AD wynosi 7 V, a błąd wynosi 0,7 V. Ten błąd nazywamy błędem kwantyzacji AD.
Dla ułatwienia analizy zakładamy, że skala (przetwornik AD) nie ma innych błędów pomiaru poza błędem kwantyzacji AD.
Teraz użyjemy dwóch identycznych skal do pomiaru dwóch napięć stałych pokazanych na rysunku 1 bez zakłóceń (sytuacja idealna) i z zakłóceniami.
Jak pokazano na rysunku 1, rzeczywiste zmierzone napięcie stałe wynosi 6,3 V. Napięcie stałe na rysunku po lewej stronie nie zawiera żadnych zakłóceń i ma stałą wartość. Rysunek po prawej stronie przedstawia prąd stały zakłócony przez prąd przemienny, a jego wartość wykazuje pewne wahania. Napięcie stałe na schemacie po prawej stronie jest równe napięciu stałemu na schemacie po lewej stronie po wyeliminowaniu sygnału zakłócającego. Czerwony kwadrat na rysunku przedstawia wynik konwersji przetwornika analogowo-cyfrowego.

Idealne napięcie stałe bez zakłóceń
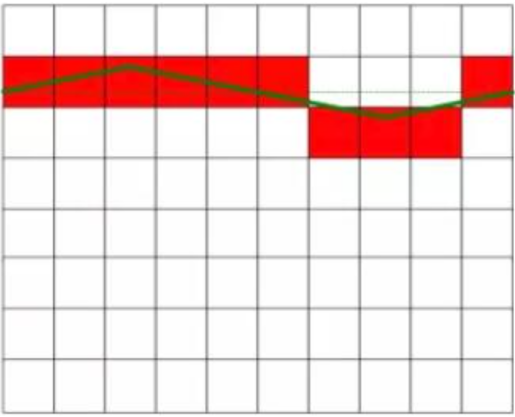
Zastosuj zakłócające napięcie stałe o średniej wartości równej zero
Wykonaj 10 pomiarów prądu stałego w dwóch przypadkach przedstawionych na powyższym rysunku, a następnie wyciągnij średnią z 10 pomiarów.
Pierwsza skala po lewej stronie jest mierzona 10 razy, a odczyty są za każdym razem takie same. Ze względu na wpływ błędu kwantyzacji AD, każdy odczyt wynosi 7 V. Po uśrednieniu 10 pomiarów wynik nadal wynosi 7 V. Błąd kwantyzacji AD wynosi 0,7 V, a błąd pomiaru 0,7 V.
Druga skala po prawej zmieniła się drastycznie:
Ze względu na różnicę dodatniego i ujemnego napięcia interferencyjnego oraz amplitudy, błąd kwantyzacji AD jest różny w różnych punktach pomiarowych. Wraz ze zmianą błędu kwantyzacji AD, wynik pomiaru AD zmienia się między 6 V a 7 V. Siedem pomiarów miało 7 V, tylko trzy 6 V, a średnia z 10 pomiarów wyniosła 6,3 V! Błąd wynosi 0 V!
W rzeczywistości żaden błąd nie jest niemożliwy, ponieważ w świecie obiektywnym nie ma ścisłego napięcia 6,3 V! Istnieją jednak:
W przypadku braku zakłóceń, ponieważ każdy wynik pomiaru jest taki sam, po uśrednieniu 10 pomiarów błąd pozostaje niezmieniony!
Przy odpowiedniej ilości zakłóceń, po uśrednieniu 10 pomiarów, błąd kwantyzacji AD zmniejsza się o rząd wielkości! Rozdzielczość poprawia się o rząd wielkości! Dokładność pomiaru również poprawia się o rząd wielkości!
Kluczowe pytania brzmią:
Czy sytuacja wygląda tak samo, gdy zmierzone napięcie przyjmuje inne wartości?
Czytelnicy mogą chcieć zastosować się do porozumienia dotyczącego zakłóceń w drugiej sekcji, wyrazić zakłócenia za pomocą serii wartości liczbowych, nałożyć zakłócenia na zmierzone napięcie, a następnie obliczyć wyniki pomiaru każdego punktu zgodnie z zasadą przenoszenia przetwornika AD, a na koniec obliczyć wartość średnią do weryfikacji, o ile amplituda zakłóceń może spowodować zmianę odczytu po kwantyzacji AD, a częstotliwość próbkowania jest wystarczająco wysoka (zmiany amplitudy zakłóceń mają proces przejściowy, a nie dwie wartości, dodatnią i ujemną), a dokładność musi zostać poprawiona!
Można udowodnić, że dopóki mierzone napięcie nie jest dokładnie liczbą całkowitą (nie istnieje w świecie obiektywnym), błąd kwantyzacji AD będzie występował niezależnie od jego wielkości. Dopóki amplituda interferencji jest większa niż błąd kwantyzacji AD lub większa niż minimalna rozdzielczość AD, wynik pomiaru będzie się zmieniał między dwiema sąsiednimi wartościami. Ponieważ interferencja jest symetryczna dodatnio i ujemnie, amplituda i prawdopodobieństwo spadku i wzrostu są równe. Dlatego im bliższa jest wartość rzeczywista, tym większe jest prawdopodobieństwo wystąpienia której wartości i po uśrednieniu będzie ona bliska której wartości.
Oznacza to, że średnia wartość wielu pomiarów (średnia wartość interferencji wynosi zero) musi być bliższa wynikowi pomiaru bez interferencji, tzn. użycie sygnału interferencji AC o średniej wartości równej zero i uśrednienie wielu pomiarów może zmniejszyć równoważne błędy kwantyzacji AD, poprawić rozdzielczość pomiaru AD i zwiększyć dokładność pomiaru!
Czas publikacji: 13 lipca 2023 r.




